Grundschwingung und Oberschwingungen in der Spektrometrie

Grundschwingungen und Oberschwingungen sind zentrale physikalische Konzepte, die die NIR-Spektrometrie überhaupt erst ermöglichen. Grund genug, sich die Prinzipien dahinter einmal etwas näher anzuschauen.

Alles schwingt

Dass Atome ständig schwingen, ist häufig noch vage aus dem Schulunterricht bekannt. Doch nicht nur Atome selbst schwingen, auch Moleküle sind keine statischen Gebilde.

Wenn Atome miteinander zu Molekülen verbunden sind, dann sind auch diese Verbindungen nicht starr, sondern flexibel, wie mit einem Gummiband oder einer Feder verbunden.

In der Physik wurden unterschiedlich komplexe Modelle entwickelt, um die Ursachen und Auswirkungen dieser Schwingungen zu beschreiben. Die wichtigsten Modelle sind der mechanische harmonische Oszillator, der quantenmechanische Oszillator und der anharmonische Oszillator. Letzterer erklärt die meisten Aspekte von echten Molekülen, ist aber mathematisch auch etwas aufwändiger. Zum Glück bauen sie aber alle aufeinander auf. Wenn wir sie uns also der Reihe nach vornehmen, dann sind sie recht gut verständlich.

Der mechanische harmonische Oszillator

Der harmonische Oszillator ist ein einfaches Modell - falsch, aber nützlich für das Grundverständnis. Es arbeitet mit einer mechanischen Vorstellung von Molekülen: Die Atome eines Moleküls werden als Kugeln visualisiert, die mit Federn miteinander verbunden sind.

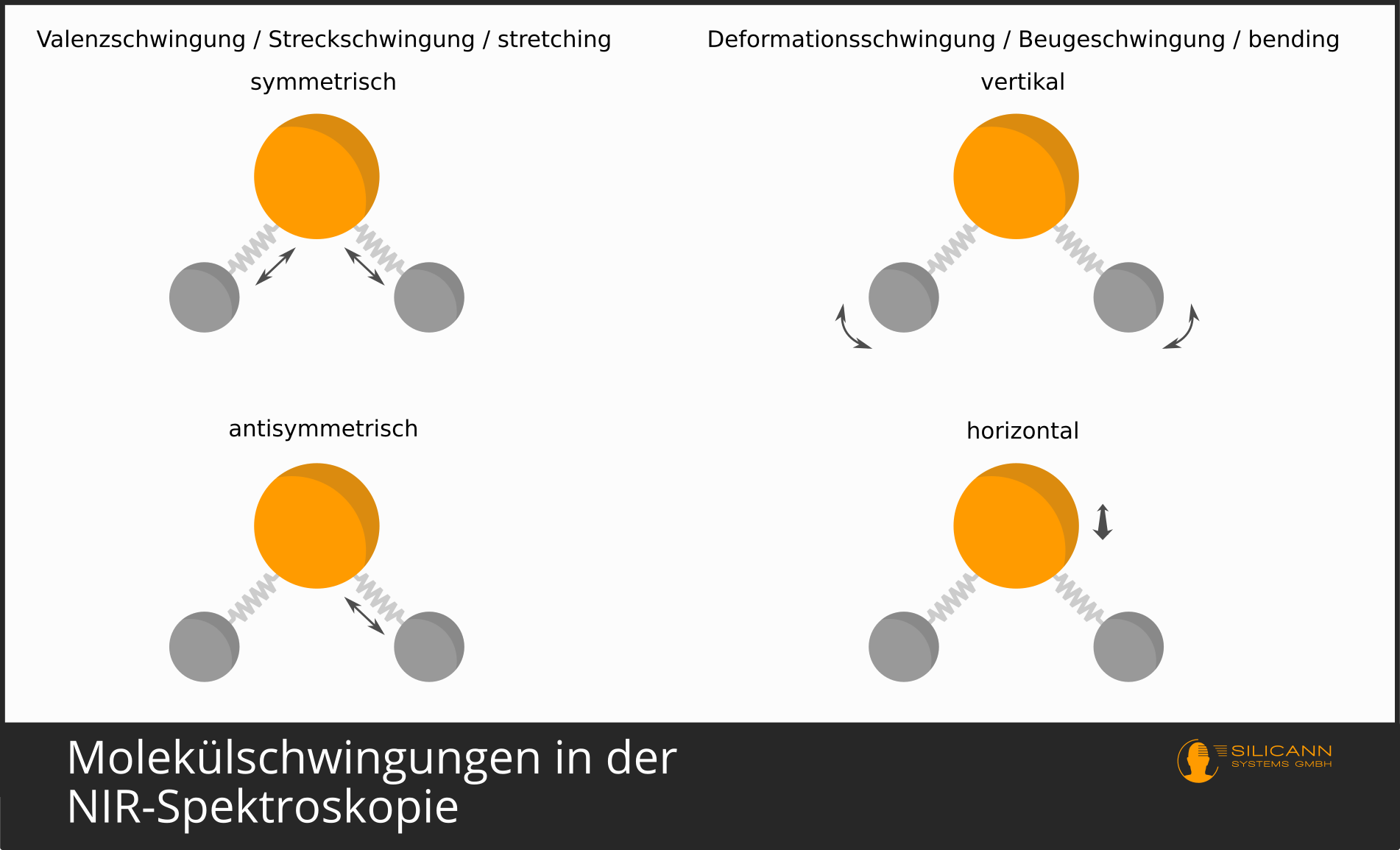
Diese Federn erlauben den verbundenen Atomen eine gewisse Flexibilität. Die Feder kann gestreckt und gestaucht werden. Das wird als Valenzschwingung bezeichnet. Ebenfalls möglich ist das Verbiegen der Feder, in diesem Fall ändert sich der Bindungswinkel der Atome. Solch eine Form der Schwingung heißt Deformationsschwingung.

Federn sind in der Mechanik vertrautes Terrain. Bei unserem Molekülmodell wird die Federkonstante aus der Mechanik einfach als Kraftkonstante \(k\) bezeichnet. Die Federkonstante beschreibt ja die Härte oder Steifheit der Feder. In der Chemie entspricht das der Stärke der Bindung zwischen den Atomen. Eine Dreifachbindung ist stärker als eine Einfachbindung - die Kraftkonstante \(k\) ist bei der Dreifachbindung größer.

Wenn wir jetzt noch eine Masse hätten, dann könnten wir einfach die Idee eines mechanischen Federpendels nutzen, bei dem sich die Schwingungsfrequenz aus Federkonstante und Masse ergibt.

Beim Federpendel ist die Feder auf der einen Seite an einer Wand befestigt, und am anderen Ende hängt die Masse. Den Luxus haben wir bei Molekülen nicht, aber wir können einen Trick benutzen.

Stellen wir uns ein einfaches Molekül mit nur 2 Atomen vor: HCl. Verbunden mit der Feder schwingen diese beiden Atome, H und Cl, also hin und her. Die Atome sind in Wirklichkeit jedoch nicht irgendwo fest an einer Wand fixiert, sondern befinden sich ja, wenn man weit genug heranzoomt, frei schwebend im Nichts. Die Atome schwingen also relativ zueinander, jedes der beiden Atome bewegt sich ein wenig hin zum anderen Atom und wieder zurück. Das Wasserstoff-Atom ist viel leichter als das Chlor-Atom und bewegt sich deshalb stärker relativ zum Chlor-Atom. Aber auch das Chlor-Atom schwingt immer noch stark genug, um nicht als feststehende Wand modelliert werden zu können.

Das wäre für das Modellieren aber sehr praktisch, denn mit einer Masse, die sich relativ zu einer festen Wand bewegt, lässt sich deutlich leichter umgehen. Als Lösung wurde hier das Konzept der reduzierten Masse \(µ\) eingeführt. Die Massen beider Atome werden hier zusammengerechnet:

\(μ = \frac {m_1 \cdot m_2}{(m_1+m_2)}\)

In der Mechanik wird die Schwingungsfrequenz folgendermaßen berechnet:

\(\omega_0 = \sqrt{\frac {D ( = Federkonstante)}{m ( = Masse)}}\)

Dieselbe Formel können wir jetzt auf das Molekül anwenden. Die verbindende Feder wird zur Molekülbindung, die Federkonstante \(D\) also zur Kraftkonstante \(k\). Und die Masse \(m\) wird zur reduzierten Masse \(µ\). Jetzt muss nur noch beachtet werden, dass \(\omega\) die Winkelgeschwindigkeit beschreibt, während wir die Frequenz \(v\) benötigen. Daher wird durch \({2\pi}\) geteilt:

\(v_{vib} = \frac{1}{2\pi} \sqrt{\frac {k}{µ}}\)

Wenn wir die Lichtgeschwindigkeit mit dieser Frequenz teilen, dann erhalten wir eine Wellenlänge - die Wellenlänge, bei der dieses angeregte Molekül schwingen würde. \(λ = \frac {c}{v}\)

Mit anderen Worten: Wenn wir die Atome des Moleküls und die Stärke der Bindung kennen, dann lässt sich so doch der Ort vorhersagen, an dem diese Molekül-Schwingung im Spektrum sichtbar wird, oder?

Der quantenmechanische harmonische Oszillator - raus aus der Mechanik

Fast. Leider ist es nicht ganz so einfach wie in diesem rein mechanischen Modell. Was an diesem Modell stimmt: Je leichter die Atome und je stärker die Bindung, desto höher die Frequenz und desto kleiner die Wellenlänge.

Ein wesentlicher Unterschied zur Wirklichkeit: Moleküle lassen nicht mit beliebigen Mengen von Energie zu beliebig starker Schwingung anregen. Stattdessen können die Moleküle nur ganz bestimmte Schwingungsniveaus einnehmen, und auch nur vom aktuellen Schwingungsniveau in das nächsthöhere bzw. -niedrigere Niveau wechseln. Sprünge über 2 und mehr Niveaus sind nicht erlaubt.

Die dafür notwendige Energie (der Schwingungsquant oder Energieabstand ΔE) haben wir eben schon beinahe berechnet - sie lautet \(hv_{vib}\). \(v_{vib}\) ist die oben hergeleitete Geschwindigkeit, nun multipliziert mit dem Planckschen Wirkungsquantum \(h\).

Weil diese Energie weiterhin auf \(v_{vib}\) basiert, ist sie deshalb auch weiterhin abhängig vom genauen Aufbau des Moleküls.

Wenn wir nicht nur den Energieabstand wissen möchten, sondern allgemein die notwendige Energie für ein bestimmtes Energieniveau, dann können wir das wie folgt berechnen:

\(E = hv_{vib} ( v + \frac{1}{2} )\)

Das \(v\) in den Klammern bezeichnet dabei die sogenannte Schwingungsquantenzahl und beschreibt schlicht das Niveau, auf das gehoben wird (siehe Illustration).

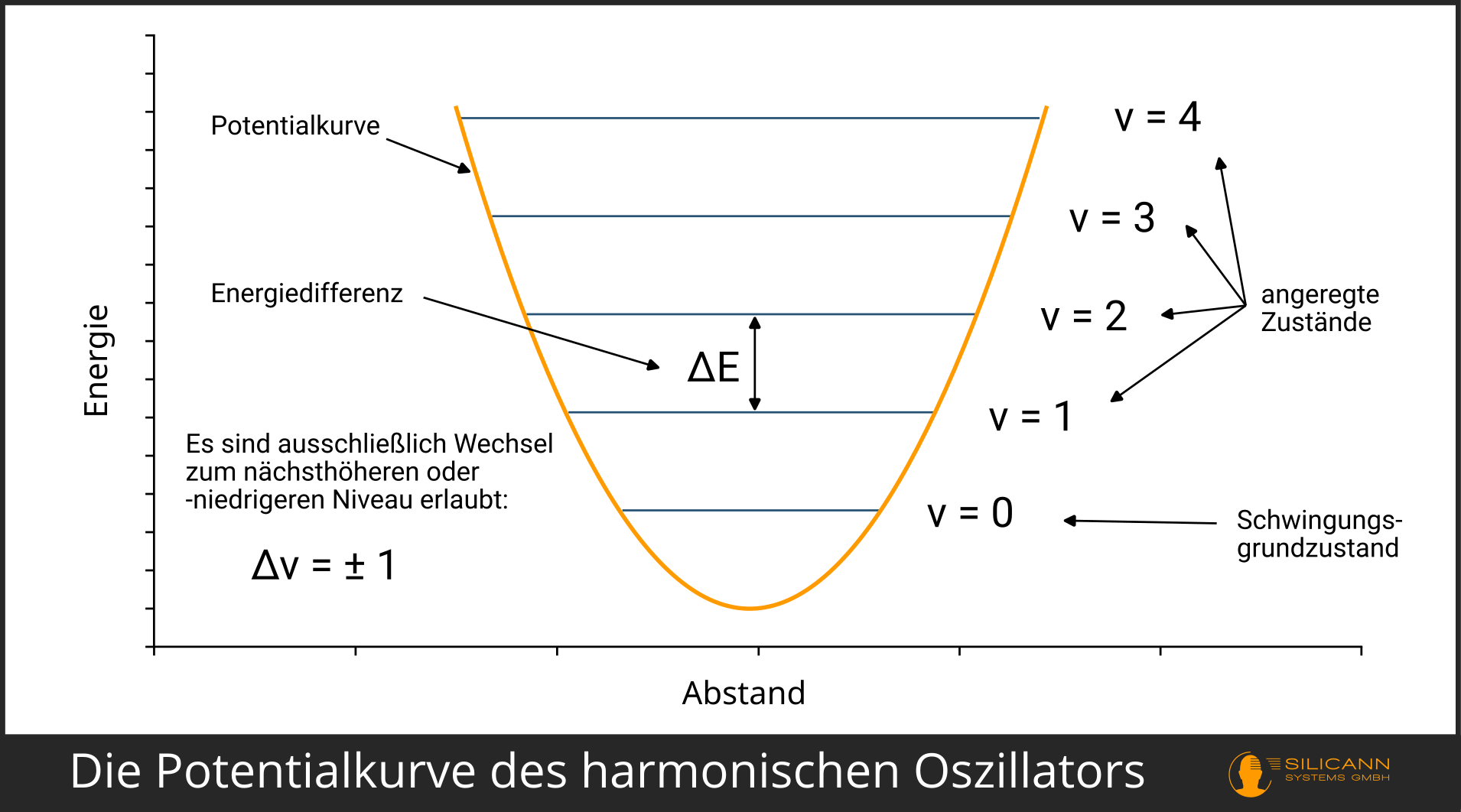
Damit beschreibt der harmonische Oszillator bereits die Funktionsweise von Schwingungen auf unterschiedlichen Niveaus. Aufgrund sogenannter Auswahlregeln kann es zwar keine Sprünge auf das z.B. übernächste Schwingungsniveau geben, aber möglich wäre immerhin eine mehrfache Anregung derselben Schwingungen (z.B. durch Zusammenstöße mit anderen Molekülen).

Da wir so ja bereits auch die Wellenlängen bestimmen können, an denen wir die Schwingungen im Spektrum sehen würden, lässt sich dieses Modell gut empirisch überprüfen. Wer dieses Experiment wirklich durchführt, wird feststellen, dass die Vielfachen der Grundschwingung nicht ganz an der "richtigen" Stelle liegen: Mit jedem weiteren Schwingungsniveau ist der Peak im Spektrum weiter in Richtung längerer Wellenlängen verschoben. Mit anderen Worten: Für jede weitere Oberschwingung ist offenbar immer weniger Energie nötig, statt exakt derselben Menge an Energie, wie das harmonische Modell vorhersagt.

Der anharmonische Oszillator

Die Ursache wird plausibel, wenn wir uns das Molekül mechanisch vorstellen. Nehmen wir ein einfaches O2-Molekül. Das eine Sauerstoff-Atom halten wir fest, das andere schwingt wild hin und her. Wir geben jetzt schrittweise immer einen weiteren Schwingungsquant hinzu, und jedes mal schwingt das lose Sauerstoff-Atom wilder. Irgendwann wird der Grenzfall eintreten: Die Schwingung ist so stark, dass das lose Sauerstoff-Atom abreißt und die beiden Atome nur noch einzeln, aber nicht mehr als Molekül existieren.

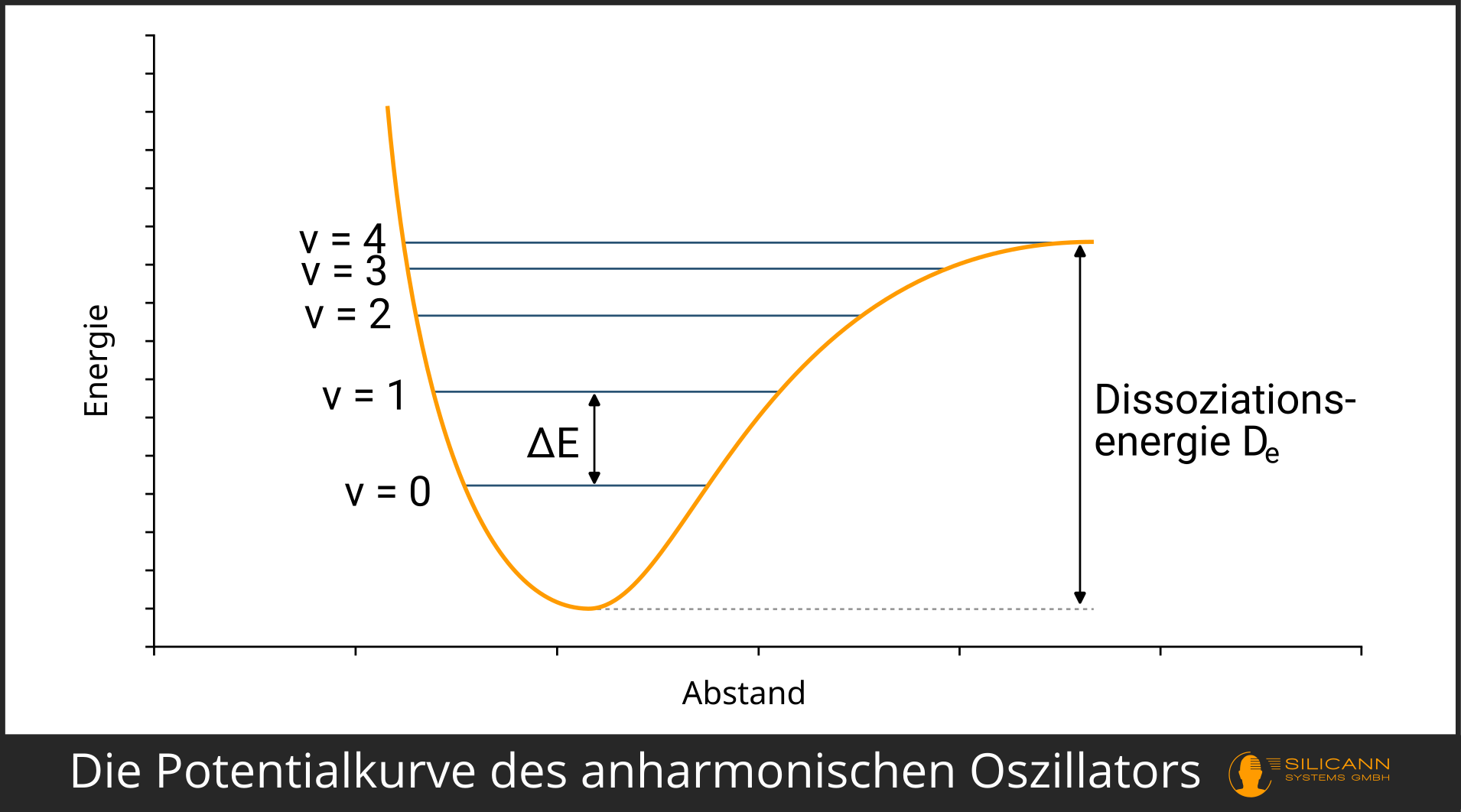
Ganz ähnlich werden die Verhältnisse im anharmonischen Oszillator modelliert. Er erweitert den harmonischen Oszillator so, dass man nicht mehr bis ins Unendliche weitere Schwingungsquanten hinzuaddieren kann, um das Molekül auf beliebig hohe Schwingungsniveaus zu heben. Stattdessen wird für jedes höhere Schwingungsniveau jeweils weniger Energie benötigt, bis das Molekül schließlich einen Punkt erreicht, an dem es dissoziiert, also aufgelöst wird. Die Energie, die dafür nötig ist, wird Dissoziationsenergie \(D_e\) genannt.

Mathematisch wird dazu die Formel von oben um eine Anharmonizitätskonstante \(x_e\) erweitert:

\(E = hv_{vib} (v + \frac{1}{2}) − h^2v^2_{vib} (v+1)^2 \frac{1}{4D_e}\)

\(D_e\) ist die einzige neu hinzugekommene Variable und beschreibt die genannte Dissoziationsenergie. Wer sich mit der Herleitung der Anharmonitätskonstante beschäftigen möchte, kann sich mit den Stichworten Morse-Kurve und Schrödinger-Gleichung auf die Reise begeben.

In der Visualisierung lässt sich sehen, dass die rechte Flanke nicht mehr bis ins Unendliche steigt, sondern auf Höhe der Dissoziationsenergie in die Waagerechte übergeht.

Grundschwingung und Oberschwingungen durch Absorption

Die Anharmonizität hat darüber hinaus weitere Konsequenzen. Allen voran ist im harmonischen Modell ein Übergang über mehrere Schwingungsniveaus (\(v = 0 \rightarrow v = 2\) usw.) nicht erlaubt gewesen, nun darf sie dagegen stattfinden. Sie wird jedoch deutlich seltener auftreten, pro übersprungenem Niveau nur zu 1-10 % im Vergleich zur Grundschwingung.

Wie wird nun das Molekül zur Schwingung angeregt? Durch elektromagnetische Strahlung. Die Photonen in der Strahlung müssen genau die Menge an Energie liefern, die dem Energieabstand ΔE entspricht. Die Energie des Photons ist proportional zur Wellenzahl, und damit ist auch die nötige Wellenlänge leicht zu berechnen (siehe Wellenzahl in Wellenlänge umrechnen).

Trifft ein Photon mit genau dieser Wellenlänge auf das Molekül, dann wird das Molekül vom Schwingungsniveau 0 auf das Niveau 1 angehoben (\(v = 0 \rightarrow v = 1\)). Das ist die Grundschwingung des Moleküls.

Im Moment der Anregung findet eine Absorption statt: Die Energie des Photons wird vom Molekül absorbiert und in eine ausgeprägtere Schwingung umgewandelt. Das ist das Grundprinzip der Infrarot-Spektrometrie: Eine Strahlungsquelle (meist eine Glühlampe oder IR-LED) sendet ein breites Spektrum von Infrarot-Wellenlängen aus, und nach dem Kontakt mit dem Molekül wird die absorbierte Wellenlänge im Spektrum fehlen bzw. geringer ausgeprägt sein. Da die exakt nötige Wellenlänge ein Resultat aus dem spezifischen Aufbau des Moleküls ist, lässt sich auf diese Weise rückschließen, welche Art von Molekül getroffen wurde. So lassen sich unbekannte Stoffe und Mischungen von Stoffen bestimmen, indem man sie mit Infrarotstrahlung bestrahlt und das Ergebnis mit einem Spektrometer auswertet.

Es kann ebenfalls passieren, wenn auch deutlich unwahrscheinlicher, dass das Molekül genug Energie aufnimmt, um ein oder gar zwei Energieniveaus zu überspringen und gleich auf dem entsprechend höheren Niveau zu landen. Dies sind dann die 1. Oberschwingung (\(v = 0 \rightarrow v = 2\)), die 2. Oberschwingung (\(v = 0 \rightarrow v = 3\)) usw.

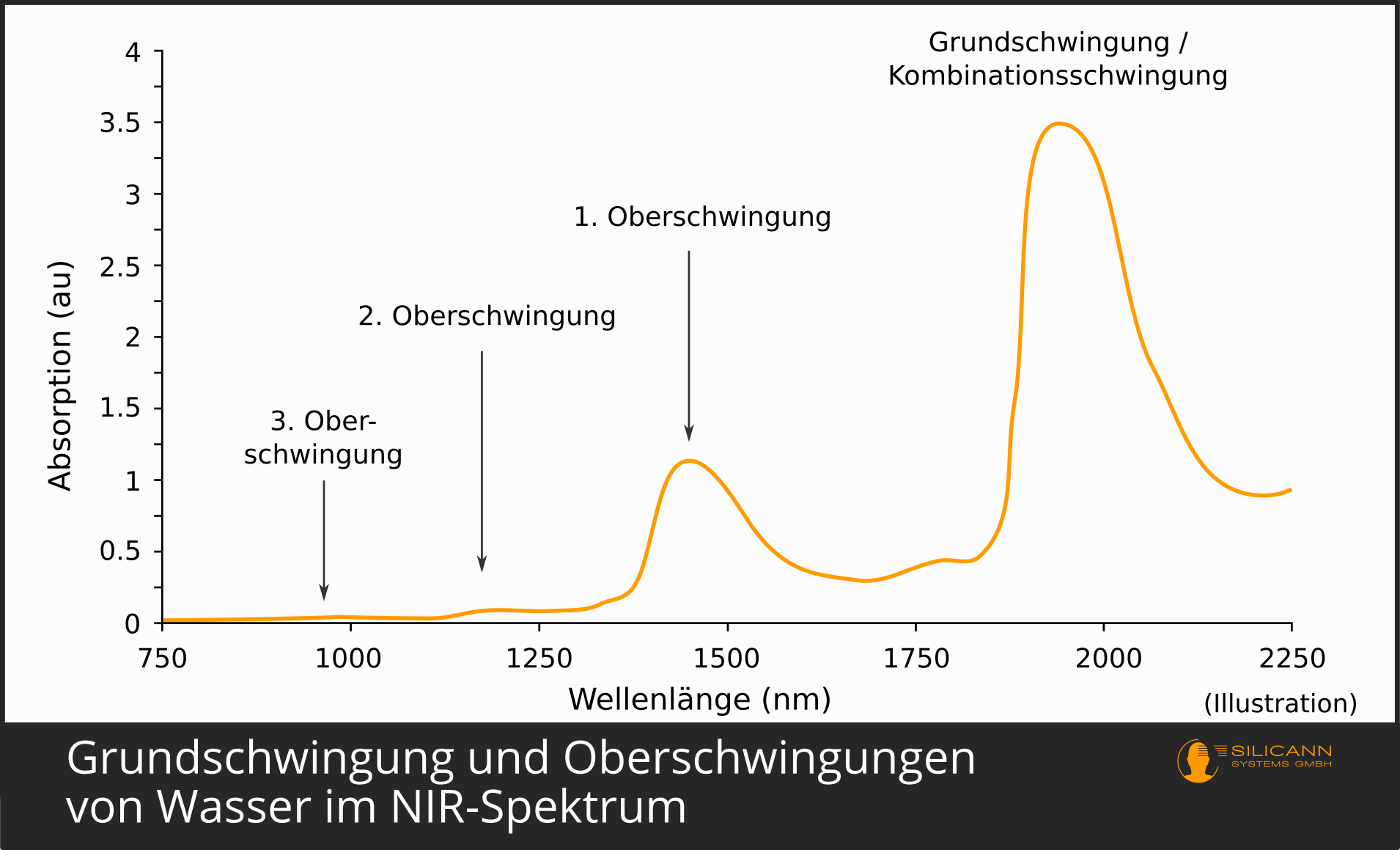
MIR vs. NIR

Die meisten Grundschwingungen liegen bei Zimmertemperatur im mittleren Infrarotbereich (MIR). Dennoch ist die Nahinfrarot-Spektrometrie deutlich verbreiteter, obwohl sie ja nur mit den weit weniger intensiven Oberschwingungen arbeiten kann. Das hat mehrere Gründe.

Zum Einen ist die hohe Absorption im MIR-Bereich sich selbst der größte Feind: Die anregende Strahlung kann deshalb nur sehr wenig in feste Materialien eindringen. Um das zu umgehen, muss die Probe z.B. in Form von Presslingen vorbereitet werden. Das ist aufwändig und teuer, und schränkt MIR-Spektrometrie deshalb im Wesentlichen auf Laboranwendungen ein, in denen höchste Präzision gefragt ist.

Außerdem absorbiert Wasser in diesem Bereich sehr stark, d.h. in feuchten Proben kann das eigentlich interessante Signal leicht durch die Schwingungen des Wasser-Moleküls überlagert werden.

Und schließlich sind viele etablierte Komponenten in der Spektroskopie nicht transparent im MIR-Bereich. Handelsübliche Glasfasern etwa absorbieren MIR-Strahlung, was sie für die Anwendung in der MIR-Spektroskopie ausschließt. Gleiches gilt für verschiedene Materialien für Linsen und andere optische Bauteile. Für beides gibt es Alternativen, aber die sind deutlich teurer.

Die NIR-Spektrometrie ist deshalb optisch und mechanisch deutlich leichter umsetzbar, und weil sie ohne Probenvorbereitung auskommt, kann sie auch kontinuierlich zur Prozessüberwachung genutzt werden (etwa über einem Fließband).

Das Dipolmoment - deshalb funktioniert NIR-Spektrometrie überhaupt nur

Kann nun jedes Molekül mit Absorptions-Spektrometrie analysiert werden? Leider nein, viele Moleküle sind nicht im Infrarot sichtbar, obwohl sich ihrem Aufbau nach eine Schwingungsfrequenz dort befinden sollte. Solche Moleküle heißen IR-inaktiv. Ob ein Molekül IR-aktiv ist oder nicht hängt von dessen genauen Form ab.

Die Form des Moleküls entscheidet nämlich, ob und wie stark die elektrische Ladung innerhalb des Moleküls räumlich getrennt ist. Das wird als Dipolmoment bezeichnet. Als Eselsbrücke kann man hier an die Pole eines Stabmagneten denken.

Ein Dipolmoment entsteht hauptsächlich aus zwei Gründen:

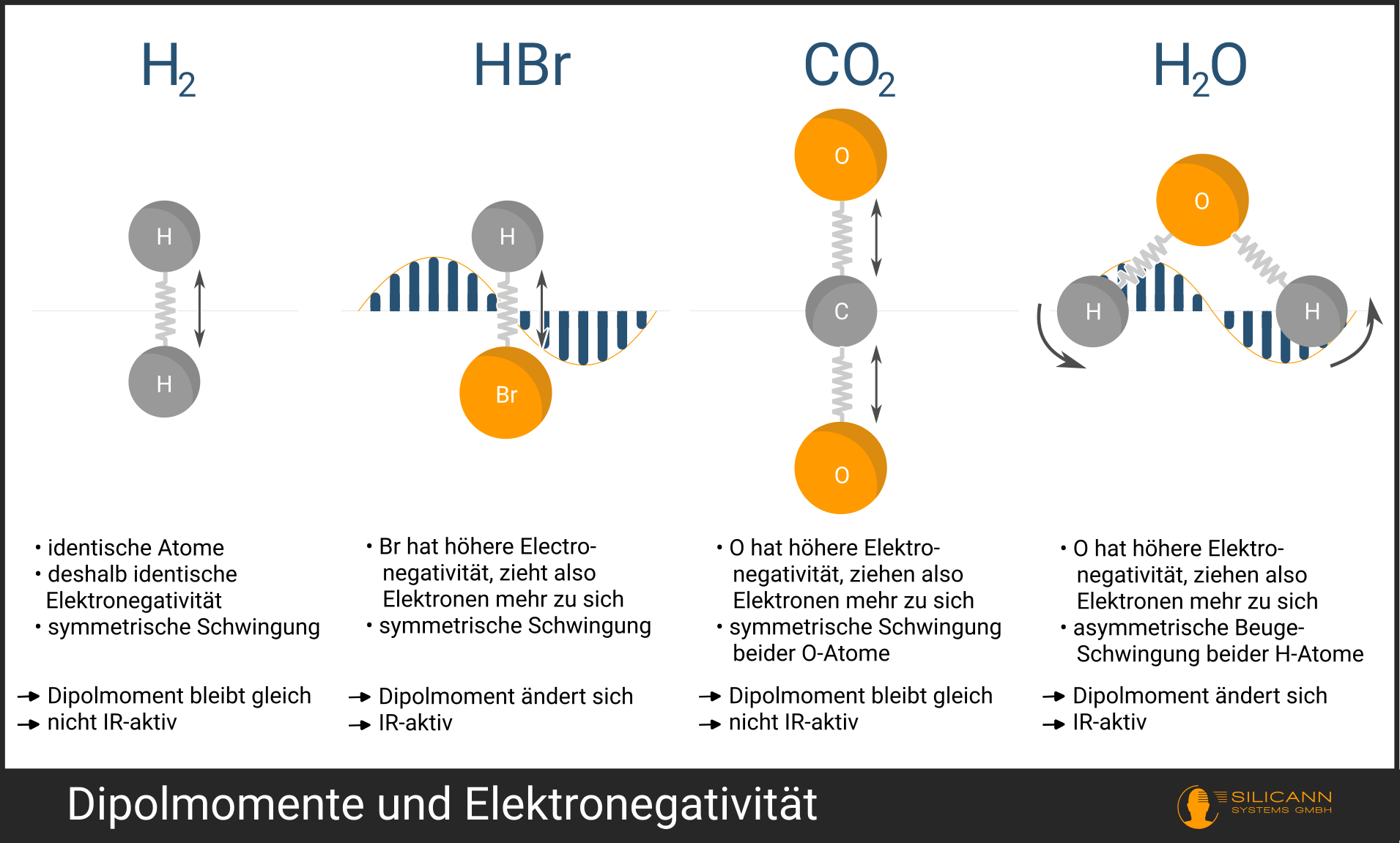
• Die Atome des Moleküls ziehen Elektronen unterschiedlich stark an. Das Stichwort hier lautet Elektronnegativität. Die Bindung von Atomen zu einem Molekül entsteht, indem sie ein oder mehrere Elektronen teilen. Die Atome sind aber ggf. unterschiedlich groß und unterschiedlich geladen, so dass die Elektronen näher an dem einen oder dem anderen Atom sind. Man spricht in diesem Fall von positiv teilgeladenen (\(δ+\)) und negativ teilgeladenen (\(δ-\)) Atomen.
• Die Geometrie des Moleküls. Das \(CO_2\)-Molekül etwa ist linear, die Atome liegen auf einer Achse. Wenn in diesem Molekül die Sauerstoff-Atome gleichzeitig eine Streckschwingung vollziehen, dann bleibt in Summe die Ladung unverändert. Beide Sauerstoff-Atome bewegen sich gleichzeitig in die genau entgegengesetzte Richtung, die beiden Teil-Ladungen heben sich genau auf. Diese Schwingung des Moleküls ist deshalb IR-inaktiv.

Damit ein Molekül Infrarot-Strahlung absorbieren kann, muss es während der Schwingung das Dipolmoment ändern. Das trifft z.B. auf das \(H_2O\)-Molekül ausgesprochen stark zu. Die Wasserstoff-Atome sind gewinkelt, und strecken sich asymmetrisch. Auf diese Weise ändert sich das Dipolmoment sehr stark im Laufe der Schwingung.

Warum ist das Dipolmoment Voraussetzung für die Sichtbarkeit in der NIR-Spektrometrie? Die Infrarotstrahlung, mit der ein Molekül bestrahlt wird, ist ein schwingendes elektrisches Feld. Als mechanisches Bild: Das Molekül wirkt wie eine Antenne - wenn es ein Dipolmoment besitzt. Das Feld der Strahlung oszilliert selbst hin und her. Wenn das Feld nach "oben" zeigt, wird die negative Seite des Moleküls auch nach "oben" und die positive Seite nach "unten" gedrückt. Dann wechselt das Feld in die entgegengesetzte Richtung und so weiter. Passiert das in derselben Frequenz wie die Schwingung des Moleküls, gibt es eine Resonanz. Und im Moment der Resonanz wird das Molekül auf ein höheres Schwingungsniveau gehoben.

Freiheitsgrade - dasselbe Molekül kann auf verschiedene Weise schwingen.

Eingangs wurde kurz angerissen, dass Moleküle auf unterschiedliche Weise schwingen können. Die Schwingungen werden in Valenzschwingungen und Deformationsschwingungen zusammengefasst.

Valenzschwingungen beschreiben das Strecken und Stauchen einer Molekülverbindung. Bei Molekülen mit einem Aufbau wie bei Wasser, also \(H_2O\), können die Wasserstoff-Atome entweder immer gleichzeitig nach innen und außen schwingen (symmetrische Streckschwingung), oder eins schwingt nach innen, während gleichzeitig das andere nach außen schwingt (asymmetrische Streckschwingung).

Bei den Deformationsschwingungen gibt es noch mehr Vielfalt. Allgemein ändert sich hier immer der Bindungswinkel zwischen den Atomen. Möglich sind hier Spreizschwingungen, Pendelschwingungen und weitere. Deformationsschwingungen sind dabei allgemein im langwelligeren IR-Bereich zu finden.

Der wichtige Punkt ist hier, dass ein einziges Molekül je nach genauem Aufbau mehrere mögliche Schwingungen aufweisen kann. Diese Möglichkeiten zur Schwingung werden als die Freiheitsgrade des Moleküls bezeichnet.

Ein einzelnes Atom im dreidimensionalen Raum kann in genau diesen drei Dimensionen schwingen. Es hat also 3 Freiheitsgrade. Ein Molekül bestehend aus \(N\) Atomen hat entsprechend potentiell \(3N\) Freiheitsgrade. Je nach konkretem Aufbau sind aber nicht alle Freiheitsgrade relevant.

Das \(CO_2\)-Molekül etwa ist linear. Eine Rotation entlang der Längsachse entfällt, denn das Trägheitsmoment ist hier null und die für die Anregung nötige Energie im Umkehrschluss unendlich. Auf diese Weise entfallen bei unterschiedlich aufgebauten Molekülen unterschiedlich viele Freiheitsgrade.

Jeder weitere Freiheitsgrad ist, Dipolmoment vorausgesetzt, eine zusätzliche Chance für eine Absorption im Infrarotbereich. Ein einzelnes Molekül kann also an mehreren verschiedenen Positionen im Spektrum auftauchen.

Diese Tatsache kann man sich sogar zunutze machen, um den chemischen Aufbau eines unbestimmten Stoffes zu bestimmen. Eine \(C-H\)-Schwingung etwa schwingt immer an derselben Stelle, egal, in welchem Molekül sie vorkommt. Mit genügend Hinweisen dieser Art lässt sich deshalb die genaue Struktur eines Moleküls entschlüsseln.

Das ist jedoch nur etwas für sehr präzise Messungen im Labor, und beispielsweise auch ein geeignetes Anwendungsfeld für die MIR-Spektrometrie. In der Praxis geht es bei der NIR-Spektrometrie meist darum, die Anwesenheit bzw. das Mischungsverhältnis bekannter Stoffe zu analysieren. Weil das im NIR-Bereich durch simples Draufleuchten auf eine Probe (verbunden mit mathematisch weniger simpler Datenverarbeitung) möglich ist, finden sich NIR-Spektrometer sehr häufig in der Qualitätskontrolle z.B. in der Nahrungsmittel-Industrie.